狄拉克函数傅里叶变换常用函数傅里叶变换

2018-01-18

字体:

大中小

浏览:

文章简介：信号与系统的基本思想:把复杂的信号用简单的信号表示,再进行研究. 怎么样来分解信号?任何信号可以用 Delta 函数的移位加权和表示.只有系统是线性时不变系统, 才可以用单位冲激函数处理, 主要讨论各个单位冲激函数移位加权的响应的叠加能得到总的响应.线性系统(齐次性,叠加定理) 时不变系统对一个系统输入单位冲激函数,得到的响应为 h(t).表征线性时不变系统的非常重要的东西, 只要知道了系统对单位冲击函数的响应, 就知道了它对任何信号的响应, 因为任何信号都可以表示为单位冲激函数的移位加

信号与系统的基本思想:把复杂的信号用简单的信号表示,再进行研究。怎么样来分解信号?任何信号可以用 Delta 函数的移位加权和表示。只有系统是线性时不变系统, 才可以用单位冲激函数处理, 主要讨论各个单位冲激函数移位加权的响应的叠加能得到总的响应。

线性系统(齐次性,叠加定理) 时不变系统对一个系统输入单位冲激函数,得到的响应为 h(t).表征线性时不变系统的非常重要的东西, 只要知道了系统对单位冲击函数的响应, 就知道了它对任何信号的响应, 因为任何信号都可以表示为单位冲激函数的移位加权和。

例如:d(t)__h(t) 那么 a*d(t-t0)__a*h(t-t0) ? ? f ( t )= ? f ( ? ) ? (t-? )d ? 的响应为 y( t )= ? f ( ? ) h ( t -? ) d ? -? -? 记为 y(t)=f(t)*h(t),称为 f(t)和 h(t)的卷积总结为两点:对于现行时不变系统,任何信号可以用单位冲激信号的移位加权和表示,任何信号的响应可以用输入函数和单位冲激函数响应的卷积来表示连续时间信号和系统的频域分析时域分析的重点是把信号分解为单位冲激函数的移位加权和, 只讨论系统对单位冲激函数的响应。

而频域的分析是把信号分解为各种不同频率的正弦函数的加权和, 只讨论系统对 sinwt 的响应。都是把信号分解为大量单一信号的组合。

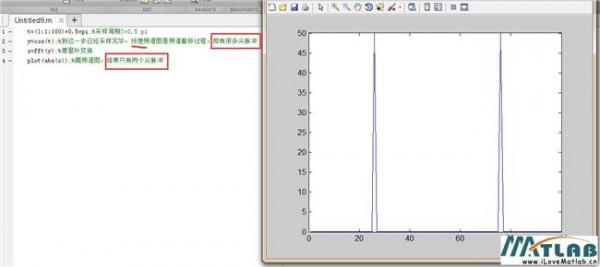
周期函数可以展开为傅里叶级数,将矩形脉冲展开成傅里叶级数,得到傅里叶级数的系数 nw 0? A ? sin x Fn = 其中 x = 。 T x 2 sin x 取样函数 S ( a )= 。产生一种震荡,0 点的值最大,然后渐渐衰减直至 0 x 第一:对于傅里叶级数的系数,n 是离散的,所以频谱也是离散状的每条谱线都出现在基波频率的整数倍上,其包络是取样函数。

nw 0? 2? 第二:谱线的间距是 w 0 .

。零点是 x = ,w 0 = 是谱的基波频率。如果 ? 不变,T 增 2 T 大,那么 w 0 减小,当 T 非常大的时候, w 0 非常小,谱线近似连续,越来越密,幅度越来越小。

傅里叶变换:非周期函数 ? 正变换: F ( jw )= ? f ( t ) e -? - iw t dt 反变换: f ( t )= 1 2? ? -? ? F (jw ) e jnw t dw 常用函数的傅里叶变换(典型非周期信号的频谱) 1、门函数 2 w? w? F ( w )= sin = ? Sa ( ) w 2 2 2、指数函数(单边) f ( t )= e u (t) - at F( w )= 1 a jw ,实际上是一个低通滤波器 3、单位冲激函数 F(w)=1,频带无限宽,是一个均匀谱 4、常数 1 ( 常数 1 是一个直流信号,所以它的频谱当然只有在 w=0 的时候才有值,体现为 ? w ) 。

F(w)=2 ?? (w) 可以由傅里叶变换的对称性得到 5、正弦函数 F( e jw0 t )= 2?? ( w -w0 ) ,相当于是直流信号的移位。 jw0 t F (sin w0 t )= F (( e F (sin w 0 t )= F (( e 6、单位冲击序列 -e - jw0 t )/ 2)= ? ( ? ( w -w0 )- ? (w w 0 )) jw0 t -e - jw0 t )/ 2 j )= ? j ( ? ( w - w 0 )- ? (w w 0 )) ? T ( t )= ? ? ( t -Tn ) -? ? 这是一个周期函数,每隔 T 出现一个冲击,周期函数的傅里叶变换是离散的 F ( ? T ( t ))=w 0 n =- ? ? ? (w -nw ? 0 )= w 0? w0 (w) 2? T 单位冲击序列的傅里叶变换仍然是周期序列,周期是 w 0 = 傅里叶变换的性质 1、线性性傅里叶变换是积分运算,而积分运算是加法。