几个重要定理的内容:梅涅劳斯定理、塞瓦定理、托勒密定理

塞瓦定理设O是ABC内任意一点,AO、BO、CO分别交对边于D、E、F,则(BD/DC)*(CE/EA)*(AF/FB)=1证法简介
()本题可利用梅涅劳斯定理证明:
ADC被直线BOE所截,
∴ (CB/BD)*(DO/OA)*(AE/EC)=1
而由ABD被直线COF所截,∴ (BC/CD)*(DO/OA)*(AF/BF)=1
:即得:(BD/DC)*(CE/EA)*(AF/FB)=1
()也可以利用面积关系证明
BD/DC=SABD/SACD=SBOD/SCOD=(SABD-SBOD)/(SACD-SCOD)=SAOB/SAOC
同理CE/EA=SBOC/ SAOB AF/FB=SAOC/SBOC
得BD/DC*CE/EA*AF/FB=1
利用塞瓦定理证明三角形三条高线必交于一点:
设三边AB、BC、AC的垂足分别为D、E、F,
根据塞瓦定理逆定理,因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA)/[(CD*ctgB)]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/
[(AE*ctgB)]=1,所以三条高CD、AE、BF交于一点。

托勒密定理
定理的提出
[编辑本段]
一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。

定理的内容
[编辑本段]
托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.
证明
[编辑本段]
(以下是推论的证明,托勒密定理可视作特殊情况。

)
在任意四边形ABCD中,连接AC,作∠BAE=∠CAD,因为∠ABE=∠ACD
则ABEACD
所以BE/CD=AB/AC,即BE·AC=AB·CD (1)
又有比例式AB/AC=AE/AD
而∠BAC=∠DAE
所以ABCAED相似.

BC/ED=AC/AD即ED·AC=BC·AD (2)
(1)+(2),得
AC(BE+ED)=AB·CD+AD·BC
又因为BE+ED≥BD
(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)
所以命题得证
推论
[编辑本段]
1.

任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,当且仅当ABCD四点共圆时取等号。

2.托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆、
推广
[编辑本段]
托勒密不等式:四边形的任两组对边乘积不小于另外一组对边的乘积,取等号当且仅当共圆或共线。
简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模,
得不等式AC·BD≤

注意:
1.等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
2.四点不限于同一平面。
欧拉定理:在一条线段上AD上,顺次标有B、C两点,则AD·BC+AB·CD=AC·BD

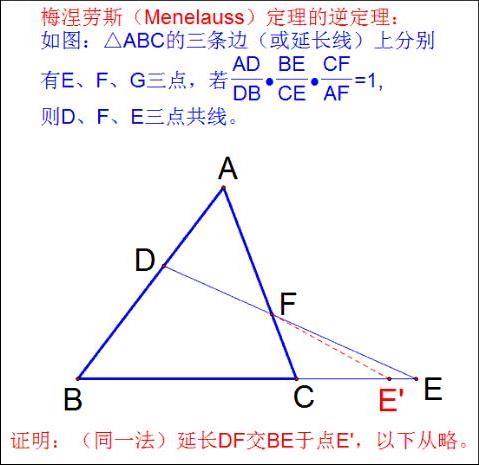
梅涅劳斯(Menelaus)定理是由古希腊数学家梅涅劳斯首先证明的。它指出:如果一条直线与ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)(BD/DC)(CE/EA)=1。证明:
过点A作AGBC交DF的延长线于G,
则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。

三式相乘得:AF/FBBD/DCCE/EA=AG/BDBD/DCDC/AG=1
它的逆定理也成立:若有三点F、D、E分别在的边AB、BC、CA或其延长线上,且满足(AF/FB)(BD/DC)(CE/EA)=1,则F、D、E三点共线。

利用这个逆定理,可以判断三点共线。

另外,有很多人会觉得书写这个公式十分烦琐,不看书根本记不住,下面从别人转来一些方法帮助书写为了说明问题,并给大家一个深刻印象,我们假定图中的A、B、C、D、E、F是六个旅游景点,各景点之间有公路相连。我们乘直升机飞到这些景点的上空,然后选择其中的任意一个景点降落。

我们换乘汽车沿公路去每一个景点游玩,最后回到出发点,直升机就停在那里等待我们回去。
我们不必考虑怎样走路程最短,只要求必须“游历”了所有的景点。

只“路过”而不停留观赏的景点,不能算是“游历”。
例如直升机降落在A点,我们从A点出发,“游历”了其它五个字母所代表的景点后,最终还要回到出发点A。
另外还有一个要求,就是同一直线上的三个景点,必须连续游过之后,才能变更到其它直线上的景点。

从A点出发的旅游方案共有四种,下面逐一说明:
方案 ——从A经过B(不停留)到F(停留),再返回B(停留),再到D(停留),之后经过B(不停留)到C(停留),再到E(停留),最后从E经过C(不停留)回到出发点A。

按照这个方案,可以写出关系式:
(AF:FB)*(BD:DC)*(CE:EA)=1。
现在,您知道应该怎样写“梅涅劳斯定理”的公式了吧。
从A点出发的旅游方案还有:
方案 ——可以简记为:A→B→F→D→E→C→A,由此可写出以下公式:
(AB:BF)*(FD:DE)*(EC:CA)=1。

从A出发还可以向“C”方向走,于是有:
方案 ——

A→C→E→D→F→B→A,由此可写出公式:(AC:CE)*(ED:DF)*(FB:BA)=1。 从A出发还有最后一个方案:
方案 ——

A→E→C→D→B→F→A,由此写出公式:(AE:EC)*(CD:DB)*(BF:FA)=1。
我们的直升机还可以选择在B、C、D、E、F任一点降落,因此就有了图中的另外一些公式。
值得注意的是,有些公式中包含了四项因式,而不是“梅涅劳斯定理”中的三项。

当直升机降落在B点时,就会有四项因式。而在C点和F点,既会有三项的公式,也会有四项的公式。公式为四项时,有的景点会游览了两次。
不知道梅涅劳斯当年是否也是这样想的,只是列出了一两个典型的公式给我们看看。