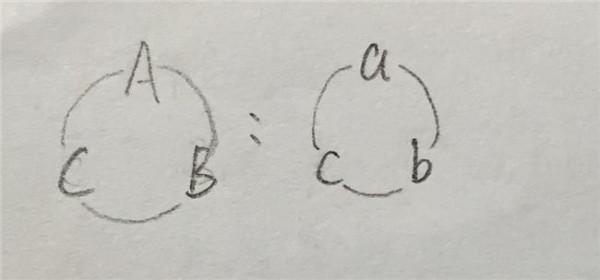徐骁的原型 一个教授逻辑学的教授 有三个非常聪明的学生 怎么猜数字的?

与某位少侠思路一样 解答过程如图 若有错误望指正 真的会有人看吗! 我都不想看了

匿名用户:

首先要理清一个容易混淆的地方,就是本题中涉及了几个角色。 最明显的是三个学生——假设他们是A、B、C,他们分配到的数是a、b、c——是游戏的主体。他们每个人的任务,都是在具体的某一局游戏当中,推测自己的数。

其实,在看到另外两人的数的那一刻,他们就会知道,自己的数不是这两数之和,就是这两数之差,肯定是这其中的一个;接下来所有的推理,都是在分辨到底是和还是差。 然后一个没什么存在感的角色是教授,负责设计游戏的三个数,让学生来猜。

教授只要随便找一个正整数加法的算式就可以了,根本不需要任何细致的推理。 最后一个角色是做题的“我们”。本题的要求是,让我们根据“在第二轮时C说出144”这个事实,来推测教授可能选用了哪个(包含144的)算式。

注意,我们的任务是找所有可能的游戏,而不是参与到具体某一局之中去推理。 明晰了不同角色的定位,就可以做题了,具体参见 @曾加 的回答,我完全赞同,不再赘述。 然而,还可以换一个角度补充几句。

让我们思考一下,假如我们是A、B、C中的一个,我们该如何玩这个游戏呢?到底是怎么推理的?下面以(36, 108, 144)为例,模拟一下三位学生的推理过程,也算是对答案的一个验证。

下文中的“!=”意思是“不等于”。 首先,教授把(36, 108, 144)三个数分配给A、B、C三人,即a = 36, b = 108, c = 144。然后开始依次询问。 第一个是A。当他看到b = 108, c = 144的时候,他就知道自己的候选集是{36, 256},自己的数a肯定是这两者中的一个。

到底是哪个,无从得知,所以他说“不确定”。 这里要注意一点,单单看到别人的两个数,一般是无法判断自己的数的,因为不知道是和还是差。

但有一种情况下能做出判断,那就是别人的两个数相等的时候。比如,你看到另外两个数都是21,那自己只能是21 21 = 42,因为21 - 21 = 0不是正整数。

“他们相等,我就是和”这一点是整个游戏的基石,是能得出定论的根本。 游戏继续,轮到B了。B看到a = 36, c = 144,也就确定了自己的候选集是{108, 180},同样无法判断自己的数b是哪个。

然后,还没完,B根据A说的“不确定”,得出了b != c的结论。也就是说,B想:“如果我是144,那A看到两个144,就会得出自己是288的结论,不会说不确定。所以我的数不是144。” 这个b !

= 144的结论,看似没有什么用,因为B的候选集{108, 180}里本来就没有144,何须再排除一次。但是,这个结论对别人是有用的,因为别人并不知道B的候选集是什么。伴随着B说的“不确定”,这个信息就流传了下去。

然后视角来到C处。C看到a = 36, b = 108,也得出了自己的候选集{72, 144}。然后,根据a的“不确定”,判断出c != b即c != 108;根据b的“不确定”,判断出c !

= a即c != 36。于是C的排除集是{108, 36}。 仅仅这些吗?不,还有最关键的一点:C还能挖掘利用【B根据A说的“不确定”得出了b != c的结论但仍然说“不确定”】这一点。C想:“B听到A说‘不确定’,应该能判断出b != c。然而,这一点并没有帮助B从他的候选集里排除一个数,所以,我的数c,并不在B的候选集里。”B的候选集是什么?是

a - c

。c不在其中,也就是说a c != c、a - c != c、c - a != c,也就是说,c != a / 2即c != 18。C的排除集扩展成了{108, 36, 18},依然和C的候选集{72, 144}交集为空,所以C也只能说“不确定”。

这样,第一圈就转完了。总结一下,三人的推理如下: A:候选集:{36, 256};排除集:{};条件:b、c;结论:不确定。 B:候选集:{108, 180};排除集:{144};条件:a、c、A不确定;结论:不确定。

C:候选集:{72, 144};排除集:{108, 36, 18};条件:a、b、A不确定、B不确定、B知道【A不确定】后仍不确定;结论:不确定。

第二回合也是相似的玩法,只是更加复杂而已。 第二轮A可利用的条件有四个: B知道【A不确定】后仍不确定; C知道【A不确定】后仍不确定; C知道【B不确定】后仍不确定; C知道【B知道『A不确定』后仍不确定】后仍不确定。 由第一个条件可知,c不在B的候选集中,即

a - c

!= c,可得a != 2c即a != 288; 由第二个条件可知,b不在C的候选集中,即

a - b

!= b,可得a != 2b即a != 216; 由第三个条件可知,a不在C的候选集中,即

a - b

!= a,可得a != b / 2即a != 54; 最后一个条件,A想:“A不确定,说明b != c,B显然意识到了这一点,但仍然没能得出定论,说明c不在B的候选集中,

a - c

!= c即c != a /2。然而这一点一定会被C意识到,但他也没能排除什么,说明a / 2不在C的候选集中,

a - b

!= a / 2可得a != 2b / 3即a != 72。” 于是,A的排除集变为{288, 216, 54, 72},仍然与A的候选集没有交集,不可排除,仍然是不确定。 然后就又轮到B了。B经过一番类似的思考后,也没能得出结论,于是就又轮到了C。

C经过复杂的思考之后,终于在排除集中出现了72,从而确定自己是144。具体的思考过程,留作习题。 总之,通过上述的模拟,证实了如果游戏真是这样,那C确实会在第二轮的时候得出自己是144的结论,从而验证了(36, 108, 144)确实是一个解。

同理,其他的4个解都可以用类似的方法验证。 习题1:思考这段分析与曾加的答案的联系。 习题2:思考这段分析与斐波那契数列的联系。

习题3:模拟第二轮中B与C的推理过程。 习题4:还有一种“假设排除法”,比如C在第一轮会想:“如果我是72,那么,……,没什么矛盾;如果我是144,那么,……,也没什么矛盾:所以不确定。”;在第二轮会想:“如果我是72,那么,……,矛盾,所以我是144。”。思考这种方法与本文方法的联系。(提示:递归与递推。)

唐嘉佳:

终于解出来啦!发现跟第一名的答案方法有些类似(相对繁琐了些),anyway,还是很开心好么,所以来跟大家分享一下~~~ 基本的思路是这样:1.答案由C在第二轮猜出(C2表示),因此A1,B1,C1,A2,B2这五轮都没有人猜出。

2.在两个可能的答案中猜出结果,意味着排除了错误的答案。3.猜出的前提是这些数之间具有的特殊联系,每次猜不出都会揭示更多的否定条件 设三个数分别为a,b,c A1;非c=b B1:非c=a, 非b=c,即非a=b c=2c,即非c=0.

5a C1:非a=b 非c=a,即非b=a a=2a,即b=2a 非c=0.5a,即非b-a=0.5a且a-b=0.5a,即非b=1.5a或b=0.

5a A2:(考虑B1,C1) 非a=c,即非b=a c=2c,即非c=0.5b 非a=2c(c=0.5a)即非b c=2c且非b-c=2c,即非c=b(重)且非c=1/3b 非a=b,即非c=a b=2b,即非c=2b 非a=0.

5b(b=2a)即非b-c=0.5b且c-b=0.5b,即非c=0.5b(重)且非c=1.5b 非a=2/3b(b=1.5a)即非b-c=2/3b且c-b=2/3b即非c=1/3b(重)且非c=5/3b 非a=2b(b=0.

5a)即非b c=2b且非c-b=2b即非c=b(重)且非c=3b B2:(考虑C1,A2) 非b=a,即非c=2a 非b=2a,即非a c=2a且非c-a=2a,即非c=a(重)且非c=3a 非b=1.

5a,即非a c=1.5a且非c-a=1.5a,即非c=0.5a(重)且非c=2.5a 非b=0.5a,即非c-a=0.5a且非a-c=0.

5a,即非c=1.5a且非c=0.5a(重) 非b=2c(c=0.5b),即非a-c=2c,即非c=1/3a 非b=3c(c=1/3b),即非a-c=3c,即非c=1/4a 非b=0.5c(c=2b),即非a-c=0.

5c,即非c=2/3a 非b=2/3c(c=1.5b),即非a-c=2/3c,即非c=3/5a 非b=3/5c(c=5/3b)即非a-c=3/5c即非c=5/8a 非b=1/3c(c=3b)即非a-c=1/3c即非c=3/4a C2:(考虑A2,B2) 非c=0.

5b, 即a-b=0.5b(a=1.5b),即c=a b=2.5b 3:2:5 非c=1/3b,即a-b=1/3b(a=4/3b),即c=7/3b 4:3:7 非c=2b,即a-b=2b(a=3b),即c=4b 3:1:4 (108,36,144) 非c=1.

5b,即a=2.5b,,即c=3.5b 5:2:7 非c=5/3b,即a=8/3b,即c=11/3b 8:3:11 非c=3b,即a=4b,c=5b 4:1:5 非c=2a,即b=3a,即c=4a 1:3:4(36,108,144) 非c=3a,即b=4a,c=5a 1:4:5 非c=2.

5a,即b=3.5a,c=4.5a 2:7:9(32:112:144) 非c=1.5a,即b=2.5a,c=3.5a 2:5:7 非c=1/3a,即b=4/3a,c=7/3a 3:4:7 非c=1/4a即b=5/4a,c=9/4a 4:5:9(64,80,144) 非c=2/3a即b=5/3a,c=8/3a 3:5:8(54,90,144) 非c=3/5a即b=8/5a,c=13/5a 5:8:13 非c=5/8a即b=13/8a,c=21/8a 8:13:21 非c=3/4a即b=7/4a,c=11/4a 4:7:11 因为a,b,c都是正整数,最终有5组满足条件的解(108,36,144),(36,108,144),(32:112:144),(64,80,144),(54,90,144)

我来写一个,思路和上面几位不太相同。 ================================ 其实一切都是从2、1、1三个数字演化而来的。 我们先约定一种表示方式:同学ABC面对面围坐在一起,各自的数除去最大公约数后为abc,表示为下图所示的符号。

(这是我自己思考时用的符号,个人感觉比直接写成三元数组的坐标形式要直观些) 如图,如果ABC分别是211,那么A1最先猜出。下面考虑由211演化出的231,在B的猜测里b可能等于1或3,在A1“不知道”的信息传递给B后,B则知道b为3,B1最先猜出。

请注意这两个过程的对应: ①B1从A1处获得信息,从而最先猜出,即有效信息从A1传递到B1; ②数字由A1最先猜出的组合211演化为由B1最先猜出的组合231,演化过程是b由另外两个数之差变成了和(因为前一种情况被A1表达的信息排除掉了,所以B1则可以最先猜出)。

如果以上过程你理解了,那么下面咱们就来类推了。

C2的猜出,向前追寻有效信息可以是A2或B2,再从A2或B2向上追寻,一直到初始有效信息,形成16条有效信息链,而C2正处于这些信息链的末端。 把这些信息传递的过程对应上数字演化过程,我们可以得到下图 根据144的质因数分解状况,找出16种数字组合中符合条件的解,最后乘上公因数便得到最终答案。

================================= 另外,用这个思路可以很容易地证明曾少侠@曾加答案中提到的结论:无论是怎样的三个初始数,在有限回合内一定有人能猜出。

我们只需要把每个数组中最大的数换成两个较小数之差(当然,必须是正数)。将这个过程不断进行下去,在有限回合内一定可以得到有两个数相等的数组。并且对应有效信息传递的过程,我们可以得出是哪位同学、在第几次回答时最先猜出。 PS: 请原谅我这狗扒一样的字 (╥﹏╥)

匿名用户:

谢邀。挺简单的,穷举即可 首先,每个人看到另外两个数字时只会得到两个预想的答案:1,两者之和;2,两者之差 那么在什么情况下,自己能够在看到另外两人的数字后立刻得知自己的是多少呢。那就是当另外两人数字是一样的时候。

所有A说,不知道,意味着提供给B和C信息是,你们俩的数字是不同的。既BC数字比值不是1:1,既ABC比值不为(2:1:1) 那么对于B,他就得到了另一个有用信息。所以如果他见到AC两人的数字其中一个是另一个的两倍,他也能立刻知道自己的数字。

既可以排除ABC比值为(1,2,1)或(2,3,1) 好了,这时候到C了,首先,他看到的A和B两个数字不一样,其次他知道自己的数字不是A的两倍,也知道自己和C的数字不一样。

但是他依然得不到结论。 也就是说,他见到的ABC的数字比例关系并不是(1,2,3)(2,3,5)(2,1,3)(1,1,2) 这时候,又回到A,他虽然第一圈下来并不知道结果,但是他听了B和C的话又得到了新的信息。

可是他还不知道,所以ABC的数字比值不是(3,2,1),(4,3,1),(5,2,3),(8,3,5),(4,1,3),(3,1,2) 然后又到了B,他依然不知道,那么由此可知,ABC比值不是(1,4,3),(2,7,5),(2,5,3),(1,3,2),(3,4,1),(4,5,1),(5,8,3),(8,13,5),(4,7,3)(3,5,2) 重点来了 这时候C突然就知道了。

也就是说,他从A或者B的第二轮得到了有用信息,那么ABC有可能的情况是:(3,2,5)(4,3,7)(5,2,7)(8,3,11),(4,1,5)(3,1,4)(1,4,5)(2,7,9)(2,5,7)(1,3,4)(3,4,7),(4,5,9)(5,8,13)(8,13,21)(4,7,11)(3,5,8) 由于是正整数,所以最后一位必须是144的因数。

那么可以排除掉许多项只剩下 (3,1,4)(2,7,9)(1,3,4)(4,5,9)(3,5,8) 分别对应 108,36,144 32,112,144 36,108,144 64,80,144 54,90,144

匿名用户:

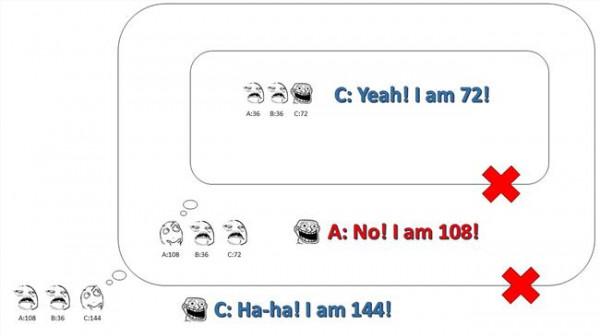
大堆文字不想看的快过来,直接看最下面的图啊! 看到题目了于是兴冲冲想来写答案,没想到和 @曾加 大神的重了,(* ￣︿￣),不开森~ 算了,补一张图吧~ 顺便回答一下 @杨海洋 同学的疑问。 具体不用多说,曾加已经说的很详细了。

这里绿色是能整除144的,灰色是不能整除144的。关于你说的那个2:7:9的,C的心理活动是这样的:具体不用多说,曾加已经说的很详细了。这里绿色是能整除144的,灰色是不能整除144的。

关于你说的那个2:7:9的,C的心理活动是这样的: A是32,B是112,我要么是80,要么是144。我如果是80的话,B刚才应该就会说,自己是112,因为B会想:“A是32,C是80,我要么是112,要么是48,我如果是48的话,那在上一轮C就会说出他是80了,因为C会想:“A是32,B是48,我要么是80,要么是16,我要是16的话,刚才B就会肯定地说自己是48了,因为B会想:“A是32,C是16,我要么是16,要么是48,我要是16的话,特么A早就赢了,所以我肯定不是16,是48没错”,(C接着想):呵呵,这点小聪明能瞒得住我,既然B刚才没说自己是48,那我就不是16而是80。

”(B接着想):嘿嘿,C这小子的想法完全在我的掌控之中,既然C上一轮没说自己是80,那我就不是48,而是112。” (C接着想:)刚才我的一套推理堪称完美,我真的是80的话,B就能够根据我上一轮没猜出自己是80而猜出他自己是112了,而且肯定还在沾沾自喜猜透了我的想法,但是看他现在愁眉苦脸的样子,看样子我不是80,而是144。

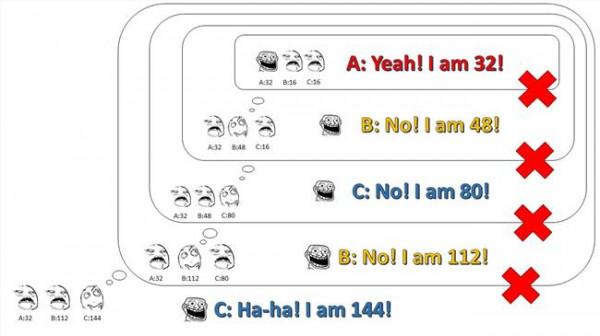
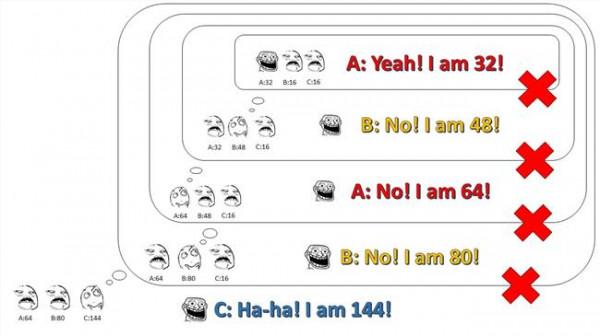
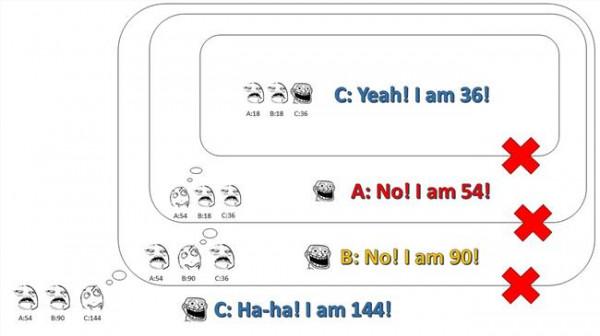
嗯,就酱~ C:老师老师!我知道了…… 今晚有什么奖励给我嘛?<(▰˘◡˘▰)> 教授:来来来~ 都把脑门伸过来,我们再换张纸条啊~ A、B、C:(/= _ =)/~┴┴ (/"≡ _ ≡)/~┴┴ (╯‵□′)╯︵┻━┻ ------------------------------------------------------------分割线--------------------------------------------------------- 补一些直观的图: (1)2阶解法之一: (2)2阶解法之二: (3)3阶解法: (4)4阶解法之一: (5)4阶解法之二:

天马:

其实这类问题有很多.所谓的"难",其实指的是在看题/理清题意上的困难,和暴力穷举时的烦琐,真正技术上来讲并不"难". 很多题目所谓的做法其实就是穷举,只是对于具体题目具体分析,可能不断会注意到某些可利用的性质,然后剪枝比较明显罢了.

. 也许某种类型的问题很常见,规则大体相同,只是具体题目有某些具体细节的差异(其实不妨说题目本身是带有一些参数的,只是定义域太大了所以随便抽都能算是一个新题). 像这样的,倒是很可能会被抽象出一些比较有效的剪枝方式,或者说,这就是这类问题的一些技巧,或者说是方法.

举个栗子,数独.所谓的数独,其实本质上也是穷举,只是被人研究太多了所以手推的时候启发函数的作用经常相当明显罢了.

. 然而还有一些问题一般并没有组成这样的大类,所以不值得/没办法抽象出一些大类里普遍适用的适合手算的"方法",比方说就这题....([s]强行把话题拉回去....[/s]) 所以我觉得这种问题所谓的手推没多大意义.

.弄出结果来就行了..抽象不出模型的东西不值得抽象出啥技巧.. 所以像"这种方法比那种方法要多试了一些结果/剪枝的时候研究得更深入细致所以一堆杂七杂八的分析后能剪掉更多"根本没意义.

. ps.既然像这种东西要弄出所谓的手推的技巧没多大意义了..那使用计算机也就没所谓了对吧..嗯,倒不如说这个问题的价值也不必那个最终能成功的程序的算法多多少.. (hmm..我就不说用prolog写程序了.

...) 说到电脑..再说回数独吧..一个好的算法对数独完全是秒的..然而手推还是有乐趣的..就是因为抽象出了很多在所有数独题目都适用的适合手推的技巧.. ################################ 每次见到这种东西就吐满肚子苦水槽于是再次强行把话题拉回原题的分割线 ################################ 记三个人依次为A,B,C,对应的数依次为a,b,c.

首先,总共有6次判断.我们依次记为P1,...,P6. 记Qi为P1且P2且...且Pi.于是,我们要求的是满足Q6的(a,b,c). 显然,对于某个i,第i次判断的那个人面对(a,b,c),会猜测自己是另两人的 和 或 差的绝对值,对应两个局面.

于是(a,b,c)满足Qi等价于对应的这两个局面都满足Q(i-1). ################################################################ # 说得比较抽象,而且毕竟不是竞赛,就不去写严谨了.

. # 举个栗子吧..对i=5,B看到(a,_,c)后会认为局面有可能是(a,a c,c)或(a,

a-c

,c). # 然后B就会想.. # "假如A看到的是(_,a c,c),会不会有多解呢..如果是看到(_,

a-c

,c)呢.. # 总之,如果两个中有哪个没有多解,那前4次就不会有这种状况了,所以肯定是另外一个,那我就能确定了." # 所以,B不能确定当且仅当这两个均对应了第四次判断的多解. ################################################################ 回到原题.

.先上一些代码吧.. 算了改变主意了不码代码了还是先直接手推吧.. [s](所以上边那堆到底是干吗的....)[/s] Q1: b<>0,c<>0,b<>c Q2: (a,a c,c),(a,

a-c

,c)均满足Q1 a<>0,b<>0,c<>0,a<>c,b<>c,a<>2c Q3: (a,b,a b),(a,b,

a-b

)均满足Q2 a<>0,b<>0,c<>0,a<>b,a<>c,b<>c,2a<>b,a<>2b,a<>2c,3a<>2b Q4: (b c,b,c),(

b-c

,b,c)均满足Q3 a<>0,b<>0,c<>0,a<>b,a<>c,b<>c,2a<>b,a<>2b,a<>2c,2b<>c,b<>2c,3b<>2c,3a<>2b,b<>3c,3b<>c,5b<>3c Q5: (a,a c,c),(a,

a-c

,c)均满足Q4 a<>0,b<>0,c<>0,a<>b,a<>c,b<>c,2a<>b,a<>2b,2a<>c,a<>2c,2b<>c,b<>2c,3a<>c,a<>3c,a<>4c,3b<>c,b<>3c,3a<>2b,3a<>2c,2a<>3c,3b<>2c,3a<>4c,5a<>2c,3a<>5c,5b<>3c,5a<>8c Q6: (a,b,a b),(a,b,

a-b

)中一个不满足Q5,一个满足Q5且对应的c=144 分两种情况.. I.a b=144,(a,b,a b)满足Q5,(a,b,

a-b

)不满足Q5. a b=144只有有限组解,故穷举可破,结果是(32,112,144),(36,108,144),(54,90,144),(64,80,144),(108,36,144). II.

a-b

=144,(a,b,

a-b

)满足Q5,(a,b,a b)不满足Q5. 从"(a,b,a b)不满足Q5"得到一个等式,再和

a-b

=144联立,经验证只有有限组解,其中使得(a,b,

a-b

)满足Q5的..没有.

匿名用户:

一个教授逻辑学的教授,有三个普通学生 一天教授给他们出了一个题,教授在每个人脑门上贴了一张纸条并告诉他们,每个人的纸条上都写了一个正整数,且某两个数的和等于第三个!(每个人可以看见另两个数,但看不见自己的) 教授问第一个学生:你能猜出自己的数吗?回答:不能 问第二个,不能 第三个,不能 再问第一个,老师你刚刚问过我一遍了...

匿名用户:

第一次回复, 私以为第一的答案有误, 欢迎讨论 第一答主的解答是通过数学模型推导而来, 之所以这道题是逻辑题而不是数学题, 我认为是因为需要考虑到实际情况, 以答主(2:7:9)的答案为例, 假设A看到另外两个人头上的数字为7和9 那么他 不用推导 都能排除掉(2:1:1),(2:3:1),(2:3:5)等等的可能性, 因为自身的数字只有 2和16两种情况, 而这两种情况, 都不能满足上述答案的比值, 那请问答主, 您又如何能从第一个人说不知道仅仅推导出不是(2:1:1)这个比值呢? 第一个人说不知道难道不是什么都无法证明吗? 因为(2 : 1 : 1)这个比值不成立, 无需证明 补充: 我认为, 该题须有一个数是另外一个数的整数倍, 即比值应为( 1 : X : X)或( X : 1 : X) ,(X : X : 1) 才可以真实的进行这个测试, 不然, 第一步都无法进行, 也就是, 问到第一个非常聪明孩子就会说 "永远也猜测不出来, 无需进行下去了"

高祤鏖:

端脑进化版?

匿名用户:

从A人猜不到只能推出B和c不一样。 B猜不到说明A和c不一样,且A不是c的两倍 c猜不到说明A和B不一样。A不是B的两倍两倍,B也不是A的两倍。 第二轮A还猜不到就说明C不是B的两倍或二分之一 B还猜不到就同上 C猜到了自己是144是因为A和B的差或和不满足上述的其中一个结论。

和肯定是满足上述结论的。就是说A和B的差不满足上述关于C的结论。A和B的差是A或B的2倍。又A和B的和是144。推的另外两个人是36和108。

表示怀疑,为什么答案只有五种?72 72=144为什么不行。私以为教授给出的正是72 72=144.当A和B看到72和144的时候肯定猜不出自己的,当C看到有两个72的时候,自己肯定是144,因为不可能有人是0。这也是为什么教授要强调正整数。

膜拜下第一的那个答案。我自己虽然有点思路但是做推论的时候脑子短路了,最后看了人家的才懂。下面跑个题试试证明下所有的(a, b, a b)都能通过这种方式推出答案(好像真的跑题挺远)。 由于问题具有对称性,所以无所谓三个人从谁开始谁的值是哪个,只要证明对任意正整数值对(a,b)命题成立即可。

并且这里的a,b没有公约数(有公约数的情况等同于约分后的情况,因为反正能看到别人卡片的数值,乘一下都一样)。 那么对任意这样的值对(a,b),(a!

=b,否则除非a和b都是1不然它们就有公约数了)只要值对(a-b,b)能构被推出,那么(a,b)也能被推出。这一步结论是根据 @曾加 的计算过程。这里由于a和b不相等,我们可以假设a>b(否则反正交换下顺序就成了)。

那么(a-b,b)也是没有公约数的正整数值对。因为假如(a-b,b)有公约数p,那(a,b)也有公约数p。(当然这里面讨论的公约数都不是1) 那么我们重复上面的过程,大的减小的,最后一定能得到值对(1,1)。

反证这一结论:如果不能得到(1,1),那么我们假设最后得到的是(i,k),其中i和k至少有一个不是1;并且i!=k,否则与(i,k)没有公约数矛盾。

那么我们仍可以用i、k中的大的减小的,与假设矛盾。 最后,由于(1,1)这一值对是能被推出来的(因为(1:1:2)可在第一轮推断出来),所以任意值对(a,b)都能通过这种方式被推断出来。 ------ 诶,数学太渣了,感觉证得好啰嗦QAQ 嘿嘿,知乎首答案。会有人理吗。。

知足老乐:

1.首先声明,最终答案还没有搞定,只能先推演一部分,有机会再更新吧。 2.感谢 @曾加答案提供思路,个人只是情景模拟。 3.推演过程描述用的是假设然后排除,可能有些混乱,大家多包涵。 一直搞不懂为什么会有分界线 一个阳光明媚的早晨,唐僧师徒4人闲着无聊,在去女儿国的路上玩起了游戏!

唐长老在仨徒弟每个人脑门上贴了一张纸条并告诉他们,每个人的纸条上都写了一个正整数,且某两个数的和等于第三个!(每个人可以看见另两个数,但看不见自己的) 教授问悟空:你能猜出自己的数吗?回答:不能 八戒,不能 沙僧,不能 再问悟空,不能 八戒,不能 沙僧:我猜出来了,是144!

唐长老很满意的笑了,于是猴子去摘桃,八戒去化斋,沙僧留下来看行李。

。。 根据已有的答案,分别为以下5组(36,108,144)(108,36,144)(54,90,144)(64,80,144)(32,112,144) 一(36,108,144)唐僧:你能猜出自己的数吗? 悟空此时心情很郁闷(以后会更郁闷):呆子是108,傻子是144,我可能是36和252,啥情报都没有,怎么玩,和尚就是偏心。

于是答道:不能 八戒有点走神:猴哥36,老沙144,我的选择有108和180,数都差不多。

。。到底是选翠兰妹妹还是嫦娥姐姐呢?于是回答:不能 沙僧此时柯南附体:A=36,B=108,C=72 or 144 ; if C=72 A无法选择正常,B看到72和36后可判断B非36(不等于号怎么打。

。。)得出B=108的答案,但是没有,不成立,排除。所以C=144。于是回答:我猜出来了,是144. 唐僧:恭喜你!都学会抢答了!。。。猴子,你拿个盒子嘀咕什么波若波罗密。

。。 二(108,36,144)回到5分钟之前的唐僧:你能猜出自己的数吗? 跟一的推演基本一致,只不过将A,B换下位置,又抢答了。。。波若波罗密。。。 三(54,90,144)又回到5分钟之前的唐僧:你能猜出自己的数吗? 悟空继续郁闷(第一个回答的总是没有任何信息提示,悲催) 八戒继续走神(翠兰和嫦娥确实不好选) 沙僧继续附体:A=54,B=90,C=36 or 144 ;if C=36 A无法选择,B思考:B=18 or 90,if B=18 A看到的是18和36,能推断出自己为54,就会给出答案,B=18不成立,所以B=90,但B也没有给出答案,C=36不成立,排除。

所以C=144.。于是回答:我猜出来了,是144 唐僧:恭喜你,虽然思考时间长了点,但还是抢答了。。。波若波罗密。。。 先更到这里,后面的推演会更长,假设也更多,还没有搞清楚,只能慢慢来了。

贴我2007年的解答,错别字就不改了 bert:关键是推理与反证,答案绝不止一种。 Update:码农,!=这两符号在一起是不等于 就当这三个人是老大、老二、老三。头上的真实数字分别是a、b、c; 第一轮分析: 第一步得出:b!

=c;(b不等于c) 第二: a!=c, a!=2c 第三部:a!=b, a!=2b, b!=2a 第二轮分析: 第一步:c!=2b, b!=2c 第二步 c!=2a,c!=3a,a!=3c; 最后一步,关键的来了: 老三想,如果我是a-b,(目的是要推出矛盾。。尝试否定a-b) 则老二就认为自己是b或者2a-b(的绝对值) 下面捏造矛盾: 若让老二猜出他的数字,则有

2a-b

= 2

a-b

---------->等式1 或者 2

2a-b

=

a-b

----------->等式2 等式1得到4a=3b;无整数解 等式2可以得到: b=3a或者3b=5a; 因为这种情况下老二可以猜出来,而事实上他没有猜出来,所以聪明的老三排除了这种情况,知道自己是两数之和。 同理也可以捏造让老大猜出数字的矛盾。得出的结果相似,只是老大老二数字换一下。 所以a、b是36与108,或者是54与90.顺序任意。

张乾坤:

叶燕赵:

刚好前几天看过类似的:国产动画《端脑》里有一集(好像是第四集还是第五集)是讲两个人各有一个数字,两个数字相乘不是8就是16,要求一个人在不能被告知对方数字的情况下猜出对方的数字。题主可以去看看,动画情景更具体,很简洁的方式就可以懂了。

可乐:

算了一下用了一个小时左右。结果分别是 108-36-144# 36-108-144# 54-90-144# 32-112-144# 64-90-144# 先说思路,这种题中假定他们都很聪明的意思是他们之间的推论都是共享的。

我们先根据回答问题的先后顺序设他们分别为ABC,先以A的角度来看,bc的值肯定不想等,如若相等,a会立即给出答案。 轮到b思考,a和c的值肯定不想等,且ac之比不能为2:1,如若不满足,B也会立即给出答案。

以此类推我们发现了一个规律,就是当一个人X思考时,X可以由前面的两个人的限定条件推出自己当前回合的限定条件,如果当前回合没有出现满足这些限定条件的数字比,那么就说不知道。

直到C说了自己是144才结束,也就是说另外两个人的数字比在C的最后一回合的限定条件中,那我们就筛选出符合条件的数字比,一共5组。 以下是我的推导过程中的各个回合的限定条件 第一回合 A 的限定条件,结果以(B:C)形式给出 1:1 B的限定条件,结果以(A:C)形式给出 1:1 2:1 C的限定条件,结果以(A:B)形式给出 1:1 2:1 1:2 2:3 第二回合 A 的限定条件,结果以(B--C)形式给出 1--2 2--1 3--1 1--3 2--3 3--5 B的限定条件,结果以(A--C)形式给出 1--2 2--3 1--3 2--5 3--2 3--1 4--1 4--3 5--3 8--5 C的限定条件,结果以(A--B)形式给出 3--1 3--2 4--3 4--1 4--5 5--8 8--13 5--2 8--3 1--3 2--5 4--7 1--4 2--7 3--5 3--4