黄琳稳定性 (线性系统的稳定性分析
关于线性系统稳定性的进一步探究任何一个实际系统总是在各种偶然和持续的干扰下运动或工作的。显然,我们首先要考虑的问题是,当系统承受这种干扰之后,能否稳妥地保持预定的运动轨迹或者工作状态,这就是稳定性。此外,我们知道,描述系统的数学模型,绝大部分都是近似的,这或者是由于量测误差,或者是为使问题简化,而不得不忽略某些次要因素。
近似的数学模型能否如实反映实际的运动,在某种意义上说,也是稳定性问题。系统的稳定性在控制中是一个很重要的问题。
在学习完稳定性理论之后,对此有了更为深刻的理解,不单单停留在输出跟踪输入的浅显印象之上,获益匪浅。因此,本文根据黄琳院士较为精炼的数学讲解,描述了一些自己对该问题的直观思考,并且结合线性系统和具体实例对稳定性作进一步分析,使内容不再过于抽象,更为深入地理解其应用价值。
1预备理论1.1微分方程解的表示考虑微分方程其解是自变量的函数,而,变动时对应的解也随着变动,故它应该是自变量与初值、的函数,可记为。
例如:问题:当初值变动时,对应的解如何变动?在应用上的意义是:初值通常是用实验方法求得的,实验测得的数据不可能绝对准确,若微小的误差会引起对应解的巨大变动,那么所求的初值问题解的实用价值就很小。
1.2Lipschitz条件的定义域记为。若存在常数L,使得对任何都有则称在上满足Lipschitz条件。这个定义可以推广到W为任意有限n维空间的情形。注:满足Lipschitz条件可保证微分方程解的存在性和唯一性1.
3解的存在性、唯一性及对初值的连续依赖性定理1-1(存在性及唯一性定理)对于微分方程若在域内连续且满足Lipschitz条件,则对任意的初始条件总存在常数,使得有唯一解,在上存在、对t连续,且满足初始条件。
稳定性所要研究的是解的渐近性质,即当解在时的性状。故总假定在上解是存在的。定理1-2(解对初值的连续依赖性)在定理1的条件下,若在域内连续且满足Lipschitz条件,则微分方程的解作为,,的函数在它的存在范围内是连续的,即,,,以上定理说明:若在初始时刻和十分接近,则在定义域内的解和也会十分接近。
因此,1.1中所提的问题也就迎刃而解了。2平衡状态的稳定性李雅普诺夫稳定性的概念是微分方程解对初值的连续依赖性这一概念在无穷时间区间上的推广和发展。
因此下面讨论时均假定所研究方程的解在无穷区间满足存在和唯一性条件。2.1平衡状态考虑系统若随着时间的变化,状态保持不变(即恒为常数),则称这个状态为系统的平衡状态。
由于平衡状态也是系统的一个状态,故它是上述微分方程的一个解,即的解。例:微分方程显然是它的一个解并且是它的一个平衡状态。2.2简化的平衡状态在初始时刻时,干扰引起的状态向量与平衡状态之差称为初始扰动向量。
由所决定的运动过程是的解,成为被扰运动,记为。由于平衡状态和被扰动运动均为微分方程的解。由此可导出扰动向量应服从微分方程称为关于平衡状态的扰动方程,即其中,满足。
这是因为因此,在下面考虑一般的时变、非线性、多变量系统时,我们总假定它的微分方程(2-1)满足(2-2)其中为n维向量,为n维的函数向量。这时方程(2-1)有解(满足),称为(2-1)的显然解或零解。
在以下讨论平衡状态的稳定性时,只需要讨论零解这个平衡状态的稳定性就可以了。2.3李雅普诺夫稳定性定义设有一个初始扰动,使系统的状态偏离了平衡状态。若初始扰动为,显然在这个初始扰动作用下,方程(2-1)所决定的运动是下列初值问题的解。
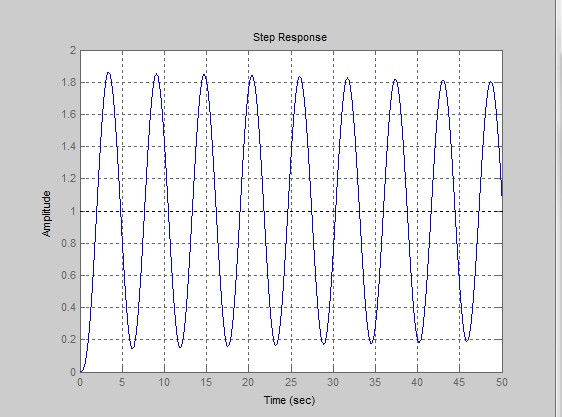
将这个解表示为。例:考虑微分方程显然,是它的一个平衡状态。现若有初始扰动则其解为。可见,即使初始值微小地偏离了平衡状态,且在任意有限的时间内其解有界,但最终将发散。
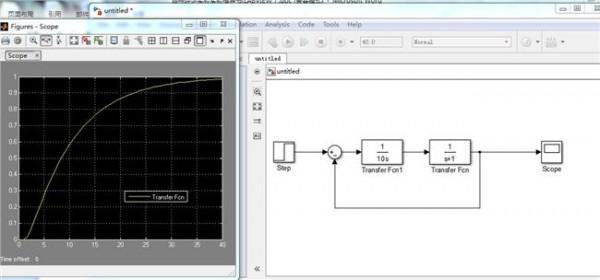
例:考虑微分方程显然是它的一个平衡状态,先若有初始扰动则其解为。事实上无论初始扰动多么大,最终将收敛到平衡状态。以上两个例子是熟悉的线性系统的稳定和不稳定的例子。从第一个例子还可以看到,尽管在任意有限的时间内解是有界的,但若讨论时间趋于无穷(或在工程上,当时间“很长”)时系统的行为,则这种发散的特性就是完全不能接受的了。
Lyapunov稳定性就是要研究微分方程的解在上的有界性。
根据微分方程解对初值的连续依赖性质,可知只要充分小,对于之间的任一时刻,偏离(平衡状态)也可以任意小。现在要研究这一性质是否对均成立。定义2-1对于任意的>0都存在,使得当时有成立。则称系统关于平衡状态(或原点)是(李雅普诺夫意义下)稳定的。
定义2-2若定义2-1中的,即与无关(关于一致),则称所定义的稳定为一致稳定。定义2-1(李雅普诺夫意义下稳定)的图示:图1李雅普诺夫意义下的稳定此处随着、而变化;,,初值变化充分小时,解的变化可任意小(不是无变化);显然,。
李雅普诺夫意义下稳定也可表示为图2李雅普诺夫意义下的稳定例如:讨论下列系统的稳定性和一致稳定性:其解为任给,取(与无关),则只